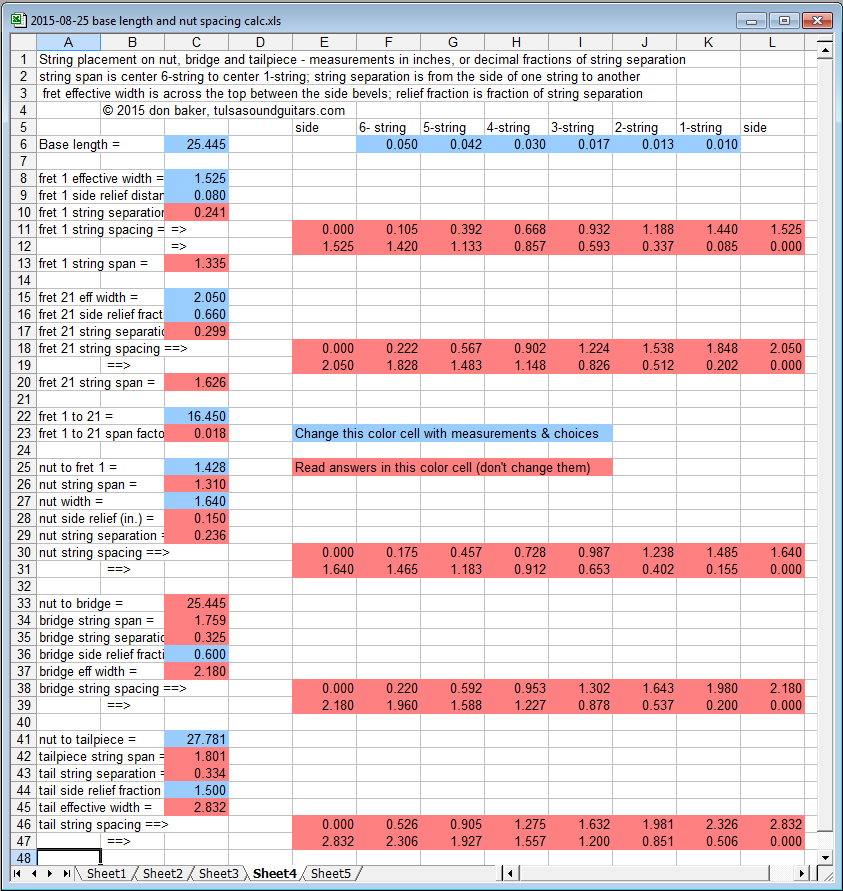
Sheets 2, 3, 4 & 5 in the spreadsheet, 2015-08-25 base length and nut spacing calc.xls, calculate the nut, bridge and tailpiece string spacing for a guitar using a Golden Gate S-96FV neck, and a string set of 0.010”, 0.013”, 0.017”, 0.030”, 0.042” and 0.050” diameters, with the base length and fret spacings fitted to measurements in Sheet 1. As noted in the spreadsheet:
1) Measurements are in inches, or in decimal fractions of the spacing between strings.
2) “String span” = center of the 6-string to the center of the 1-string.
3) “String separation” = distance from the side of one string to the side of the next.
4) “Fret effective width” = distance across the top of the fret, between side bevels.
5) “Relief fraction” = distance from the outer sides of the outer strings to the ends of the fret effective widths in terms of a fraction of the string separation.
6) The blue cells are input cells, measurements and choices.
7) The red cells are calculation output cells, and should not be changed.
8) “Span factor” = factor increase in the string span per inch going from the nut to the neck (inch/inch).
Sheet 2
Row 6 begins with the base length, 25.445”, and the string diameters. Cell C8 is the effective width of fret 1, 1.525”, and cell 9 is the relief distance (not fraction), 0.080”. In row 11, the string spacing across the top of fret 1, from the string 6 end, taking string diameters into account, so that the spacing between the sides of any two adjacent strings is equal, 0.241”, and the distance from strings 1 and 6 to the effective ends of the fret are 0.080”. Row 12 makes the same calculations from the string 1 end. The resulting fret 1 string spacing, center 6 to center 1, is 1.335”.
To calculate the angular spread of the strings to the nut, bridge and tailpiece, one more set of string spacing must be calculated. In Sheet 2, that is determined by the effective width of fret 12 and the fraction of side relief, 0.500s time the string spacing. Using these two numbers and the string diameters, Sheet 2 calculates the string spacing on fret 12 in rows 18 and 19, using the same methods for rows 11 and 12. It also calculates the string spacing on fret 12 as 0.287” and the string span as 1.565”.
The fret 1 to fret 12 “span factor” is then the difference between the fret 12 span and the fret 1 span, divided by the distance from fret 1 to fret 12. This span factor then determines the decrease in span from fret 1 back to the nut, and the increase in span from the nut to the bridge and the nut to the tailpiece. Given that span at each position, Sheet 2 again uses the string diameters and the span to calculate equal distances between the sides of the strings, and equal distances between the sides of the 1 and 6 strings to the ends of the nut, bridge and tailpiece, respectively. Not being fretted by the player, the nut, bridge and tailpiece are not taken to have bevels on their ends that affect the calculations.
In rows 33 to 39 of Sheet 2, the bridge string span is calculated as 1.825”, from the nut string span and the span factor of 0.020. Using the string diameters and a bridge side relief fraction of 0.750, Sheet 2 calculates a bridge width of 2.363” with a string spacing of 0.339”, side to side. Rows 38 and 39 show the spacing of string centers from one side of the bridge to the other, both ways.
Sheet 2 repeats those calculations for a tailpiece positioned 27.781” from the nut, with a side relief factor of 1.500. It gives and effective tailpiece width of 2.947” with string spacings in rows 46 and 47.
Sheet 3
Sheet 3 does the same thing as Sheet 2, but uses fret 21 instead of fret 12. It optimizes the fret 21 side relief factor to produce a bridge width of 2.25”.
Sheet 4
Sheet 4 does the same thing as Sheet 3, but changes the fret 21 side relief fraction (cell C16) from 0.691 to 0.660, and the bridge side relief fraction (cell C36) from 0.750 to 0.600.
Sheet 5
Sheet 5 does the same thing as Sheet 4, but changes the fret 21 side relief fraction (cell C16) from 0.660 to 0.501 to get a bridge string span (cell C34) of 1.875; changes the bridge side relief fraction (cell C36) from 0.600 to 0.495 to get a bridge effective width (cell C37) of 2.25”; and changes the tailpiece side relief fraction (cell C44) from 1.500 to 1.495 to get a tailpiece width of 3.000”. For the prototype guitar in mind, this simplifies certain construction details. In this case, the bridge string span is about 1/8” to 3/16” smaller than the usual 2” to 2-1/16” bridge spans, meant to provide a little more room for bending the 1 and 6 strings along the neck.
Summary
The insertion of 17 different measurements and choices produces string spacings at five different locations, the nut, fret 1, fret 12 or 21, the bridge and the tailpiece. In practice the elements under construction, the nut, bridge and tailpiece, can be marked from each end towards the center with a dial caliper, three marks on a side. The spacings are compensated for string diameter, so that the spacing between the sides of the strings are equal, and from the sides of strings 1 and 6 to the ends are equal.
Note – There are some small, unintentional errors in these calculations. The spacings at two points along the neck, frets 1 and 12 in Sheets 2, and frets 1 and 21 in Sheets 3 to 5, should have determined the spacings at the other locations without compensating for the diameters of the strings, merely by extending the angular projections of the strings up and down the neck. But these calculations came easier. So, when using compensated spacings at the nut and tailpiece to set the string spacing along the neck, the string spacings at frets 1 and 12 or frets 1 and 21 will be slightly off, but not a noticeable amount. It is not easy to file the nut and tailpiece slots perfectly on the marked string centers; those errors are likely more significant.